Electronic and Spectroscopic Properties of Olefins

For more information, read here.

According to the particle-in-a-box approximation for the electron energy levels of conjugated olefins, the energy level of a orbital is expressed by Eqn 1.  In this equation, n is the quantum number for the energy level, h is Plancks constant, m is the mass of the electron, and L is length of the box.  This is the 1-dimensional box model and being defined by only a length is a fair model for a conjugated olefin.

Eqn 1.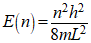    

The intensity of a transition of an electron between energy levels is determined by several factors, transition operators, population, symmetry etc.  However, one that has a high population and a small energy gap is the transition between the HOMO and the LUMO - the HOMO is occupied and the LUMO is vacant. In general, this energy gap is expressed by Eqn 2.

Eqn 2.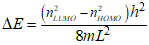    

When atomic orbitals (AO's) interact according to LCAO theory, the atomic orbital wave-functions are added together in-phase and out-of-phase, a set of molecular orbitals (MO's) result.  When the AO's are added together, the resultant quantity of MO's is always equal to the quantity of AO's.  The difference between the MO's lies in the phase of the composite AO's.  The Born-rule requires each orbital to have a maximum population of two electrons, and the electrons from the AO's fill up the MO's as per the aufbau principle - lowest energy first and then amongst the same level where several orbitals are degenerate.  For alkenes, the double-bond Pi-system MO's are composed from the parallel p-orbitals from each carbon atom, each occupied by a single electron.  Hence, the number of electrons in the resultant MO's is equal to the number constituent AO's, and since each MO can hold two-electrons, then from N p-orbitals are produced N Pi-orbitals, and containing N electrons with two-electrons in the lowest energy N / 2 orbitals and zero electrons in the upper N / 2 MO's.

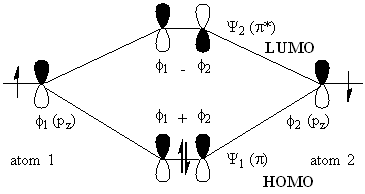
Before we continue to rationalise the N / 2 term, let use consider the valence MO-diagram for ethene (Diagram 1).  We can ignore the inner "core" electrons as these do not affect the bonding i.e., are not frontier orbitals.  With two carbon atoms, each with a p_z orbital occupied by a single electron, the resultant orbital-set will be occupied by two electrons.  When orbitals interact, the total number of orbitals does not change, so with two p_z orbitals added together in unique combinations give a set containing a number of orbitals equal to the number of intreacting orbitals.  When two orbitals have a common symmetry they will interact, with one combination where the phases match being of lower energy (the bond), and an anti-phase combination being the higher energy anti-bond.  For the purposes of this discussion, the idea of a bond and an anti-bond is not particularly important; instead we have interest primarily in the HOMO and the LUMO and their energies.  For ethene, there are two p_z orbitals, thus N = 2, and these interact to produce two new orbitals, Psi1 (pi) and Psi2 (pi*).  Populating these orbitals with the two electrons, according to the aufbau and Pauli exclusion principles, has the two electrons occupying Psi1 - the pi bonding orbital; the higher energy Psi2 orbital is vacant.  Note that N = 2, and that there are two MO's, 1 and 2; further note that orbitals numbered up to and including N / 2 are occuied, and those numbered above N / 2 are vacant. Thus, Psi _{N / 2} is the highest occupied MO and Psi _{N / 2+1} is the lowest unoccupied orbital.

It is worth noting that the anti-phase combination is higher energy than the in-phase combination, further more, the LUMO is more positive than the HOMO is negative relative to the p-orbital energy.

Diagram 1.   

 

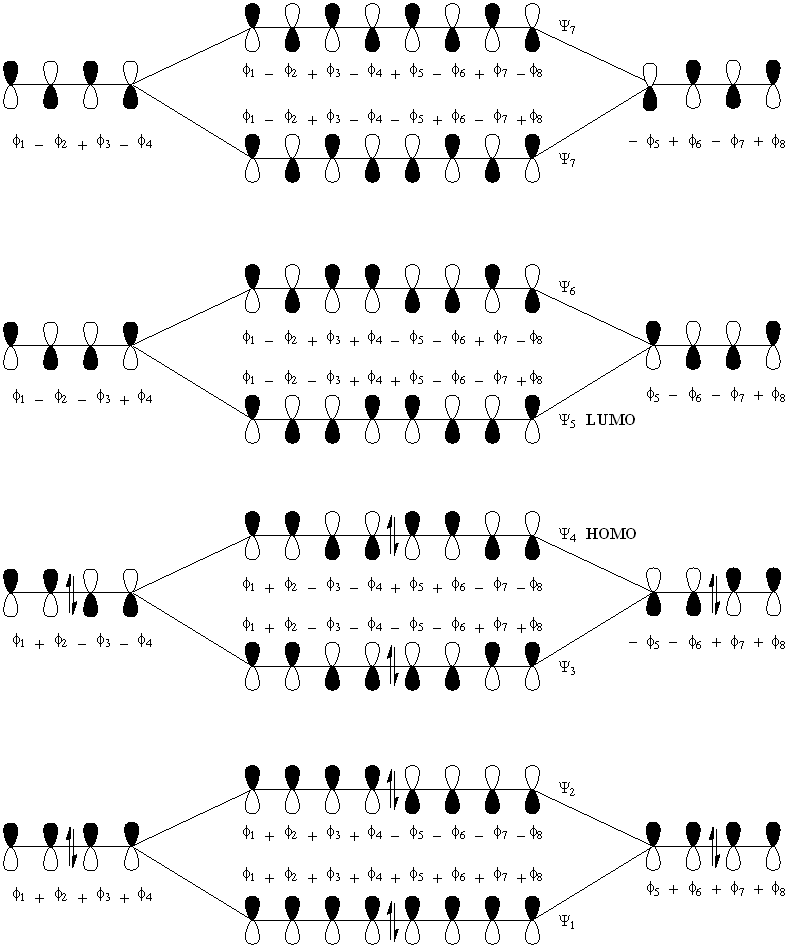
Next consider buta-1,3-diene. With four constituent p-orbitals, N = 4.  Hence there are four resultant pi-orbitals of which the lower N / 2 = two MO's are occupied by two-electrons, and the remaining two MO's of higher energy are empty.  These orbitals are denoted n = 1 to 4, with the HOMO being n = 2 and the LUMO being n = 3.  To construct the MO diagram, we will treat the butadiene molecule as a kind of dimer of ethene, adding two sets of C₂ units together (diagram2).

Diagram 2.

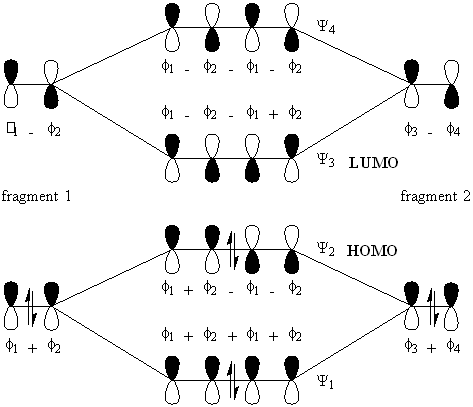
Next consider octa-1,3,5,7-tetraene (diagram 3). For this, N = 8.  Hence, the HOMO is the Psi _{N / 2} = Psi₄ orbital and the LUMO is Psi₅.

Diagram 3.